7447. Cut a string

Given a string s. You are allowed to choose any two identical adjacent characters and delete them from the string. This operation can be repeated as long as it is possible.

Before performing this operation, you may delete any number of characters from the string.

Determine the minimum number of characters that must be deleted beforehand so that afterwards, by applying the allowed operation, you can obtain an empty string.

Input. One string s (1 ≤ |s| ≤ 100).

Output. Print the minimum number of characters that must be deleted beforehand.

Sample input	Sample output
abacdeec	2

SOLUTION

dynamic programming

Algorithm analysis

Let dp[l][r] = f(l, r) be the minimum number of characters that need to be deleted from the substring s_l … s_r so that, by performing the allowed operations (removing two identical adjacent characters), we can obtain an empty string. Then:

· f(l, r) = 0, if l > r;

· f(l, l) = 1, since the single character must be deleted in advance;

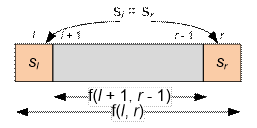
· f(l, r) = f(l + 1, r – 1), if s[l] = s[r]. In this case, the inner part of the substring is deleted first, after which the boundary characters become adjacent and can be removed;

· f(l, r) = 1 + f(l + 1, r), if the first character is deleted;

· f(l, r) = 1 + f(l, r – 1), if the last character is deleted;

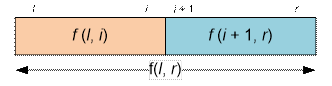
However, both of these cases can be conveniently generalized as follows: to solve the problem on the segment [l; r], split it into two subsegments [l; i] and [i + 1; r] (l ≤ i < r) and choose the minimum value:

f(l, r) =

For example:

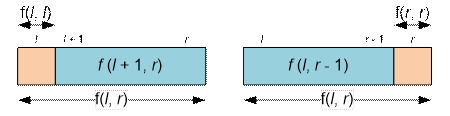
· deleting the first character is equivalent to choosing i = l (f(l, l) = 1);

· deleting the last character is equivalent to choosing i = r – 1 (f(r, r) = 1)

The answer to the problem will be dp[0][n – 1] = f(0, n – 1), where n is the length of the input string.

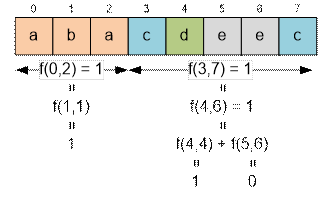
Example

Let’s consider the example given in the problem statement. We have:

f(0, 7) = f(0, 2) + f(3, 7) = 1 + 1 = 2

Algorithm implementation

Let's declare the constants and the array.

#define MAX 101

#define INF 0x3F3F3F3F

int dp[MAX][MAX];

The function f solves the problem on the segment [l; r].

int f(int l, int r)

{

if (l > r) return 0;

if (l == r) return 1;

if (dp[l][r] != INF) return dp[l][r];

int &res = dp[l][r];

if (s[l] == s[r])

res = min(res, f(l + 1, r - 1));

for (int i = l; i < r; i++)

res = min(res, f(l, i) + f(i + 1, r));

return res;

}

The main part of the program. Read the input string.

cin >> s;

memset(dp,0x3F,sizeof(dp));

Compute and print the result f(0, n – 1), where n is the length of the string s.

printf("%d\n",f(0, s.size() - 1));

Java implementation

import java.util.*;

public class Main

{

static String s;

static int dp[][];

static int f(int l, int r)

{

if (l > r) return 0;

if (l == r) return 1;

if (dp[l][r] != Integer.MAX_VALUE) return dp[l][r];

int res = dp[l][r];

if (s.charAt(l) == s.charAt(r))

res = Math.min(res, f(l + 1, r - 1));

for (int i = l; i < r; i++)

res = Math.min(res, f(l, i) + f(i + 1, r));

return dp[l][r] = res;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

s = con.nextLine();

int n = s.length();

dp = new int[n][n];

for(int i = 0; i < n; i++)

for(int j = 0; j < n; j++)

dp[i][j] = Integer.MAX_VALUE;

System.out.println(f(0, n - 1));

con.close();

}

}

Python implementation

Declare the constant INF.

INF = float('inf')

The function f solves the problem on the segment [l; r].

def f(l, r):

if l > r: return 0

if l == r: return 1

if dp[l][r] != INF:

return dp[l][r]

res = dp[l][r]

if s[l] == s[r]:

res = min(res, f(l + 1, r - 1))

for i in range(l, r):

res = min(res, f(l, i) + f(i + 1, r))

dp[l][r] = res

return res

The main part of the program. Read the input string s and compute its length n.

s = input()

n = len(s)

Initialize the list dp.

dp = [[INF] * n for _ in range(n)]

Compute and print the result f(0, n – 1).

print(f(0, n - 1))